Yksinkertaisia tähtimalleja Auringolle
Tomi Hyvönen
Aurinko ja suuri osa yötaivaalla loistavista tähdistä viettävät parhaillaan aikaansa vakaassa ja pitkäkestoisessa tilassa, pääsarjassa. Ne fuusioivat rauhalliseen tahtiin vetyä heliumiksi energiaa tuottaen. Pääsarjatähdissä kaasun paineen ja gravitaation välinen hydrostaattinen tasapaino pitää tähden vakaana. Hydrostaattisen tasapainon avulla voidaan mallintaa Auringon fysikaalisia ominaisuuksia. Vaikka näin saadut tähtimallit ovat yksinkertaisia, antavat ne kuitenkin pienin ponnistuksin hyvän kuvan Auringon fysikaalisista ominaisuuksista.
 |
| Kuva © Kari A. Kuure. |
Hydrostaattinen tasapaino
Tähden tiivistyessä tähtienvälisestä pöly- ja kaasupilvestä prototähden ydin kuumenee. Ytimen kuumentuessa riittävästi tähden ydinfuusio käynnistyy ja tähti asettuu massansa mukaiseen paikkaan pääsarjassa. Pääsarjavaiheessa tähti tuottaa energiaa fuusioimalla ytimessään vetyä heliumiksi. Se on tähden kehityskaaren ylivoimaisesti pisin ajanjakso. Auringolla pääsarjavaihe kestää noin 10 miljardia vuotta. Nyt viiden miljardin vuoden ikäisenä Aurinko on pääsarjavaiheensa puolivälissä. Mitä raskaampi tähti on, sitä lyhyempi on sen elinkaari, massiivisimmilla tähdillä pääsarjavaihe kestää vain muutamia miljoonia vuosia.
Pääsarjassa olevan tähden vakaa tila johtuu kahden voiman, gravitaation ja kaasun paineen, tasapainosta. Tähden kaasu pyrkii oman gravitaationsa vaikutuksesta rutistamaan tähteä kasaan. Toisaalta kuuman kaasun liike-energiasta johtuva paine aiheuttaa vastakkaissuuntaisen voiman. Hydrostaattisessa tasapainossa gravitaation ja kaasun paineen aiheuttamat voimat ovat yhtä suuret, mutta vastakkaissuuntaiset.
Tarkastellaan hyvin ohutta (paksuus dr ja pinta-ala dA) kaasuelementtiä tähden sisällä etäisyydellä r tähden keskustasta (kuva 1).
Tämä on ensimmäinen ja tärkein yhtälö, joka otetaan mukaan työkalupakkiin.
Otetaan lisäksi mukaan yhtälö, joka kertoo, miten tähden massa m kasvaa säteen r muuttuessa. Tähden massa saadaan tiheyden r(r) avulla yhtälöstä
Huomautettakoon, että hydrostaattisen tasapainon yhtälö ei yleisesti riitä mallintamaan tähden rakennetta. Tarvitaan lisäehtoja mm. energian tuotannosta ja energian siirtymisestä tähden läpi. Hydrostaattisen tasapainon avulla saadaan kuitenkin laskettua yksinkertaisia tähtimalleja silloin, kun tiedetään joko kaasun tiheys säteen funktiona r(r) tai tiheys paineen funktiona r(P). Tarkastellaan näitä kahta mallia tässä tarinassa hieman lähemmin. Mallit ovat yksinkertaistuksia, mutta erityisesti jälkimmäinen antaa kuitenkin hyvän käsityksen tähdissä vallitsevista olosuhteista. Tarkoituksena on kahvipöytäkeskustelun tasoisesti vastata kysymykseen, miten voimme tietää, millaiset olosuhteet Auringossa ja taivaalla tuikkivissa tähdissä todellisuudessa on?
Tähden keskustan paine ja lämpötila Pc, Tc
Kirjoitetaan hydrostaattisen tasapainon yhtälön oikea puoli sijoittamalla M(r) = M ja r = R. Käytetään tiheyden arvona tähden keskimääräistä tiheyttä . Tähden keskustan paineelle saadaan arvio
Kirjoitetaan paine Auringon massan ja säteen avulla
Pc ≈ 1015 Pa.
Paine on 10 miljardia kertaa suurempi kuin ilmakehän paine! Tulos on suuruusluokaltaan suhteellisen hyvin sopusoinnussa tarkempien tähtimallien antamien tulosten kanssa P⊙ = 2,5·1016 Pa. Hyvin yksinkertaisista lähtökohdista saatu arvio osoittaa, että Auringon keskustassa vallitsee hyvin suuri paine.
Tähden säteen ja massan välillä on relaatio R ~ Ma. Indeksi a riippuu tähden massasta, mutta käytetään keskimääräistä arvoa a = 0,8. Sijoitetaan relaatio edellä olevaan keskustan paineen lausekkeeseen. Tästä saadaan arvio keskustan paineelle tähden massan funktiona Pc ~ M-1,2. Paine laskee tähden massan kasvaessa, koska tähden säde kasvaa. Relaatiota on verrattu tähtimallien antamiin tuloksiin eri spektrityypin tähdillä kuvassa 2.
Koska kaasun tiheys pienenee säteen kasvaessa, keskustan tiheys on suurempi kuin keskimääräinen tiheys . Näin ollen lämpötilan ylärajaksi saadaan
K
Aurinkoa tai taivaalla tuikkivia tähtiä tuijottaessa on hyvin vaikea sanoa mitään perusteltua arviota tähden keskustassa vallitsevista olosuhteista. Vaikka edellä lasketut arvot eivät tarkkoja arvoja olekaan, yksinkertaisista lähtökohdista perusfysiikan avulla saa kuitenkin helposti johdettua perustellut suuruusluokka-arviot Auringon keskustan olosuhteille. Lisäksi saaduista paineen ja lämpötilan yhtälöistä nähdään, miten ne skaalautuvat tähden massan ja säteen mukaan.
Lineaarinen tähtimalli
Tarkastellaan seuraavaksi tilannetta, kun tähden tiheys säteen funktiona tiedetään. Oletetaan, että kaasun tiheys pienenee lineaarisesti keskustasta ulospäin mentäessä. Tällöin tähden tiheys on
jossa R on tähden säde on ja r etäisyys tähden keskipisteestä. Tähden tiheys keskustassa r(0) = rc ja pinnalla r(R) = 0.
Lasketaan lineaarisen mallin perusteella, miten tähden paine P(r) ja lämpötila T(r). Työkaluina ovat hydrostaattisen tasapainon yhtälö, massan yhtälö ja ideaalikaasun tilanyhtälö.
Ratkaistaan aluksi massan yhtälöstä tähden massa säteen funktiona. Sijoitetaan yhtälön dm = 4pr2rdr tiheyden paikalle lineaarisen mallin tiheys r(r)
Integroimalla saadaan
Tähden kokonaismassa M saadaan sijoittamalla r = R
Tästä saadaan ratkaistua tähden keskustan tiheys rc
Sijoitetaan r(r) ja m(r) hydrostaattisen tasapainon yhtälöön dP/dr = -Gm(r)r/r2. Integroimalla saadaan paine säteen funktiona P(r). Lasku on suoraviivainen, mutta hieman pitkä, joten luettavuuden säilyttämiseksi kirjoitetaan lopputulos ilman välivaiheita. Tähden paine säteen funktiona on
Ratkaistaan keskustan paine Pc sijoittamalla yhtälöön r = R. Tähden pinnalla paine on nolla P(R) = 0. Tähden keskustan paine on
Sijoitetaan yhtälöön keskustan tiheys rc, jolloin keskustan paine on
Pa
Yhtälöstä huomataan, että paine skaalautuu massan ja säteen suhteen samoin kuin edellä hydrostaattisesta tasapainosta saatu relaatio P ~ M2/R4.
Verrataan lineaarisen mallin mukaista painetta Auringon standardimallista interpoloituun paineeseen (kuva 4). Huomataan, että lineaarinen malli ei kuvaa painetta kovinkaan hyvin.
Kuva 4. Lineaarisen mallin mukainen Auringon paine säteen funktiona.
Lämpötila T(r) on esitetty kuvassa 5. Auringon keskustan lämpötila saadaan, kun sijoitetaan r = 0
Tc ~ 6·106 K.
Kuva 5. Lineaarisen mallin mukainen Auringon lämpötila säteen funktiona.
Lineaarinen malli ei ole käyttökelpoinen mallintamaan Auringon painetta ja lämpötilaa.
Polytrooppiset tähtimallit
jossa P on paine, r tiheys, K ja n vakioita. Polytrooppisesta tilanyhtälöstä yhdessä hydrostaattisen tasapainon yhtälön kanssa johdettuja tähtimalleja kutsutaan polytrooppisiksi tähtimalleiksi. Menneinä vuosikymmeninä niitä on käytetty tähtien mallintamiseen erittäin paljon. Ne ovat yksinkertaisia, mutta antavat kuitenkin hyvän kuvan tähtien rakenteesta. Niillä voidaan kuvata pääsarjatähtien rakennetta, mutta ne soveltuvat myös esimerkiksi valkoisten kääpiöiden mallintamiseen.
Polytrooppisen tähtimallin yhtälö saadaan johdettua hydrostaattisen tasapainon ja massajakauman yhtälöistä yhdessä polytrooppisen tilanyhtälön kanssa. Lopputuloksena saadaan kuuluisa Lane–Emden -yhtälö (J. H. Lane 1819 – 1880, R. Emden 1862 – 1940)
Yhtälössä tiheys ja säde esitetään muuttujien q ja x avulla (a on vakio)
ja
Jotta polytrooppisen tähden rakenne saadaan laskettua, Lane–Emden -yhtälö täytyy ratkaista. Yhtälön ratkaisuna saadaan Lane–Emdenin funktio q = q(x). Tähden keskustassa x = 0 ja q = 1. Tähden pinta saavutetaan Lane–Emdenin funktion ensimmäisessä nollakohdassa q(x1) = 0. Yhtälö voidaan ratkaista analyyttisesti vain tapauksissa n = 0, 1, 5. Muissa tapauksissa ratkaisu täytyy laskea numeerisesti. Yhtälön ratkaisuja eri indeksin n arvoilla on esitetty kuvassa 6.
Ratkaisu n = 0 kuvaa tähteä, jonka tiheys on vakio. Ratkaisu n = 5 kuvaa kappaletta, jonka säde on ääretön. Säde on äärellinen vain, kun n < 5.
Pääsarjatähdillä polytrooppi-indeksi n = 3 on yleisesti käytetty. Vakio K riippuu tähden massasta ja säteestä. Lasketaan polytrooppisella mallilla Auringon P(r), r(r), m(r) ja T(r). Alkuarvoina ovat Auringon massa M = 2·1030 kg ja säde R = 7·108 m.
Auringon polytrooppinen malli (n = 3)
Tiheysprofiili r(r): Kun keskustan tiheys tiedetään, tiheys säteen funktiona on
r(r)=rcq3(x)
Muistetaan edeltä, että x = ar. Vakio a saadaan laskettua nollakohdan x1 ja Auringon säteen avulla x1 = aR. Tästä saadaan a = x1/R = 9,9·104 m-1. Säde auringon säteinä on r = x/aR.
Kuvassa 7 on esitetty Auringon tiheysprofiili. Huomataan, että tiheys pienenee nopeasti säteen kasvaessa. Tiheys on pudonnut puoleen etäisyydellä ~0,2R.
K saadaan laskettua yhtälöstä keskustan tiheyden rc ja vakion a avulla
Kuten edeltä muistetaan, keskustassa q = 1. Nyt keskustan paine on
Pa
Tämä on hyvin sopusoinnussa Auringon todellisen paineen P⊙ = 2,5·1016 Pa kanssa.
Paineprofiili saadaan laskettua säteen funktiona P(r) = Pcqn+1 (kuva 9). Paine laskee nopeasti säteen kasvaessa.
Lämpötila on varsin hyvin sopusoinnussa Auringon standardimallin antaman lämpötilan (1,5·107 K) kanssa.
Lämpötila säteen funktiona (kuva 10) saadaan laskettua keskustan tiheyden ja q(x) avulla
T(r) = Tcq(x).
Yhteenveto
Yhteenvetona voidaan todeta, että polytrooppinen malli (n = 3) kuvaa kaikessa yksinkertaisuudessaan hyvin Auringon rakennetta (taulukko 2).
Lopuksi huomautettakoon että tähdillä paineeseen vaikuttaa kaasun paineen lisäksi myös säteilypaine. Mitä raskaampi tähti sitä suurempi on säteilypaineen osuus. Auringon massaisilla tähdillä säteilypaine voidaan jättää huomioimatta, kuten tässä on tehty.





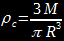














Kommentit
Lähetä kommentti
Kaikki kommentit tarkastetaan ja toimituksen harkinnan mukaan päätetään niiden julkaisusta. Aiheeseen sopimattomia tai muutoin kelvottomia tekstejä ei julkaista.